别院牧志知识库
佚名
2021-03-11
目录

Python 中的 MRO 与多继承

# 预备知识

# MRO（Method Resolution Order）

即方法解析顺序，是 python 中用于处理二义性问题的算法。

Python 语言包含了很多优秀的特性，其中多重继承就是其中之一，但是多重继承会引发很多问题，比如二义性，Python 中一切皆引用，这使得他不会像 C++一样使用虚基类处理基类对象重复的问题，但是如果父类存在同名函数的时候还是会产生二义性，Python 中处理这种问题的方法就是 MRO。

# 二义性

Python 支持多继承，多继承的语言往往会遇到以下两类二义性的问题：

  1. 有两个基类 A 和 B，A 和 B 都定义了方法 f()，C 继承 A 和 B，那么调用 C 的 f()方法时会出现不确定。
  2. 有一个基类 A，定义了方法 f()，B 类和 C 类继承了 A 类（的 f()方法），D 类继承了 B 和 C 类，那么出现一个问题，D 不知道应该继承 B 的 f()方法还是 C 的 f()方法。

C++也是支持多继承的语言之一。

对于问题 1，C++中通过同名覆盖的方式来解决，子类方法和属性会优先调用，如果要在子类中访问被屏蔽的基类成员，应使用基类名来限定（BaseClassName::Func()）。 对于问题 2，C++中通过虚继承来解决，以 virtual 关键字修饰共同的直接基类，从而保证不会产生多个基类副本产生歧义。 Python 中通过 C3 算法很好的避免了以上两类二义性的情况。

DFS

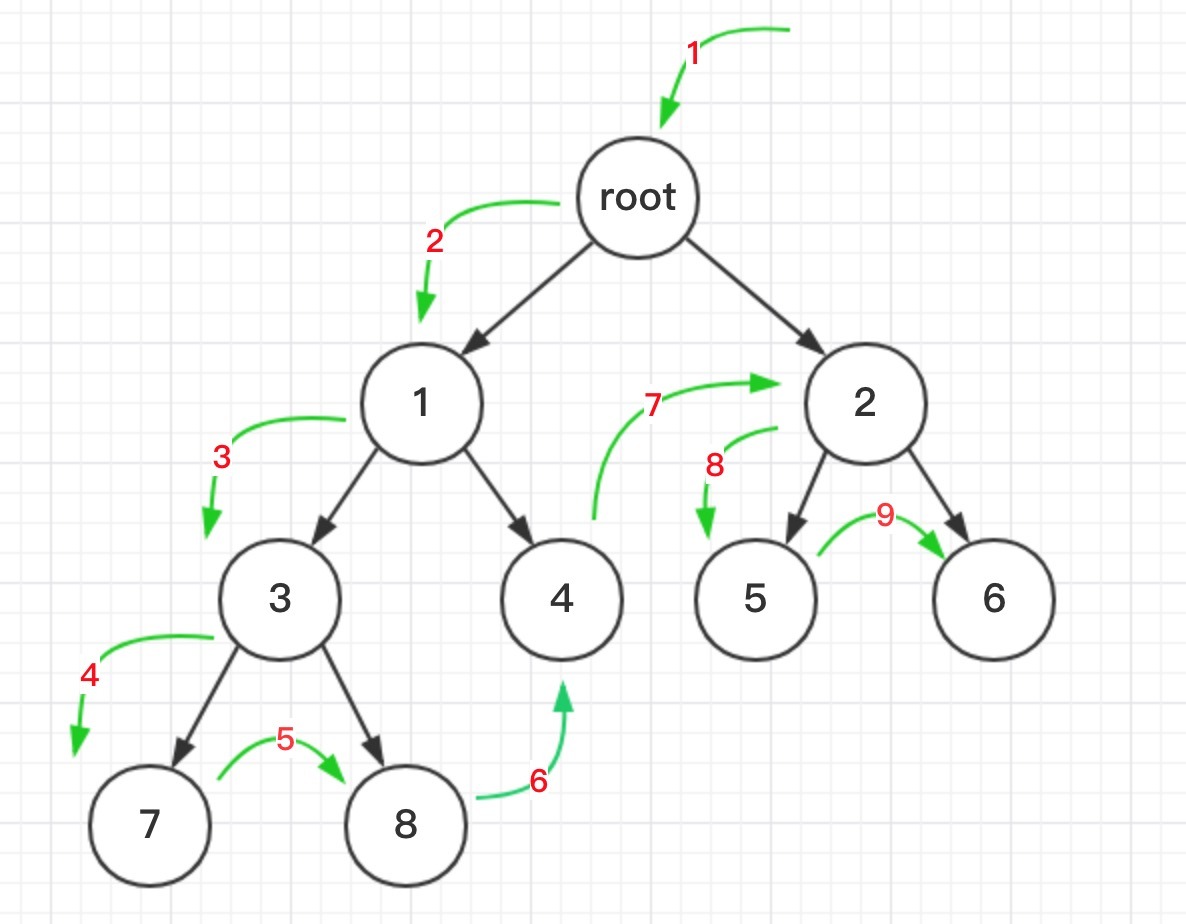
  1. 把根节点压入栈中。
  2. 每次从栈中弹出一个元素，搜索所有在它下一级的元素，把这些元素压入栈中。并把这个元素记为它下一级元素的前驱。
  3. 找到所要找的元素时结束程序。
  4. 如果遍历整个树还没有找到，结束程序。

BFS

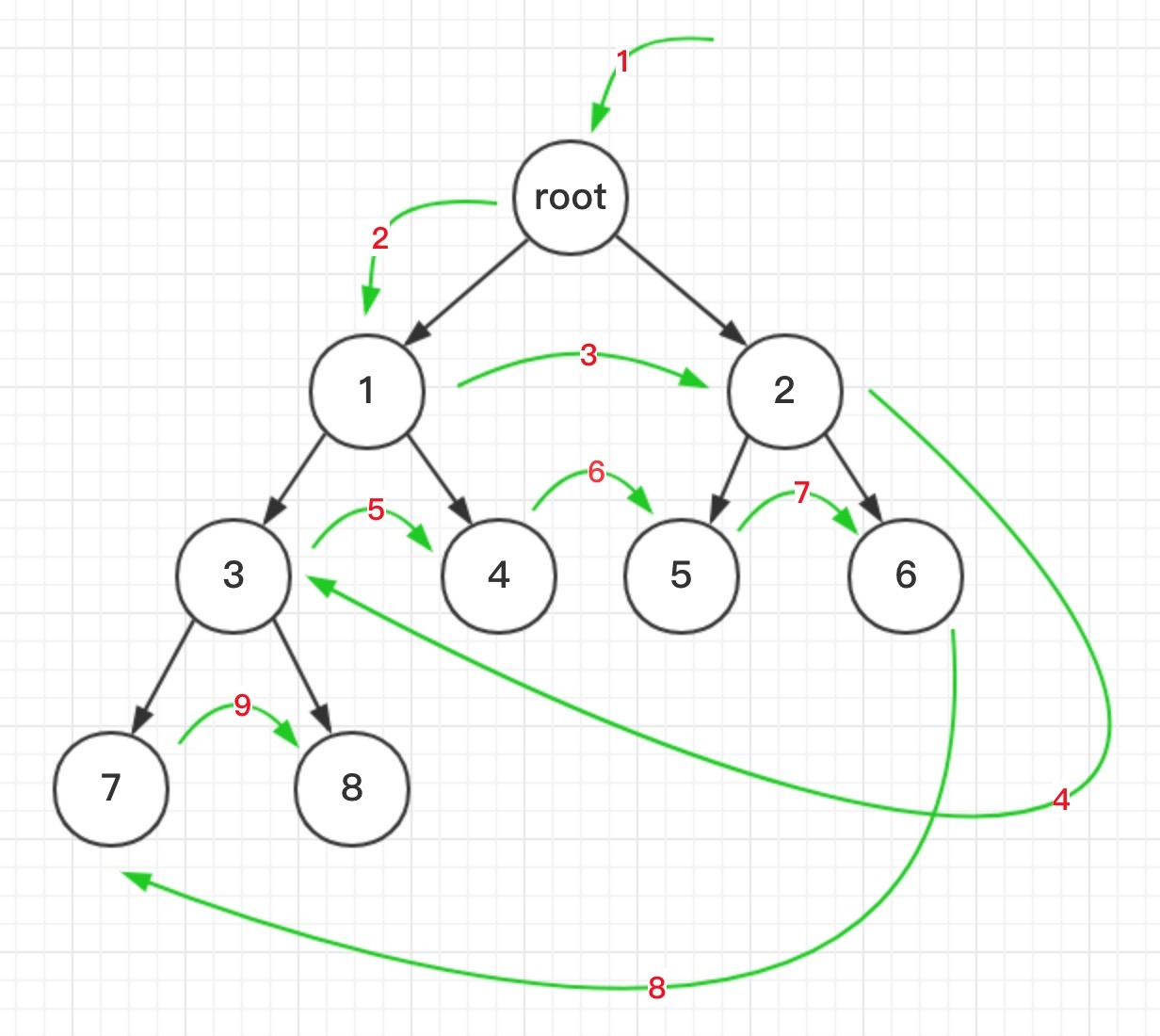
  1. 把根节点放到队列的末尾。
  2. 每次从队列的头部取出一个元素，查看这个元素所有的下一级元素，把它们放到队列的末尾。并把这个元素记为它下一级元素的前驱。
  3. 找到所要找的元素时结束程序。
  4. 如果遍历整个树还没有找到，结束程序。

# 拓扑排序

对一个有向无环图(Directed Acyclic Graph 简称 DAG)G 进行拓扑排序，是将 G 中所有顶点排成一个线性序列，使得图中任意一对顶点 u 和 v，若边(u,v)∈E(G)，则 u 在线性序列中出现在 v 之前。通常，这样的线性序列称为满足拓扑排序(TopologicalOrder)的序列，简称拓扑序列。

拓扑排序的实现步骤：

  1. 循环执行以下两步，直到不存在入度为 0 的顶点为止
  2. 选择一个入度为 0 的顶点并输出之；
  3. 从网中删除此顶点及所有出边。

# 历史中的 MRO

如果不想了解历史，只想知道现在的 MRO 可以直接看最后的 C3 算法，不过 C3 所解决的问题都是历史遗留问题，了解问题，才能解决问题，建议先看历史中 MRO 的演化。

  • Python2.2 以前的版本：经典类（classic class）时代

经典类是一种没有继承的类，实例类型都是 type 类型，如果经典类被作为父类，子类调用父类的构造函数时会出错。
这时 MRO 的方法为 DFS（深度优先搜索（子节点顺序：从左到右））。

class A:   # 是没有继承任何父类的
    def __init__(self):
        print "这是经典类"

inspect.getmro（A）可以查看经典类的MRO顺序

import inspect

class D:
    pass

class C(D):
    pass

class B(D):
    pass

class A(B, C):
    pass

if __name__ == '__main__':
    print inspect.getmro(A)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
>>  (<class __main__.A at 0x10e0e5530>, <class __main__.B at 0x10e0e54c8>, <class __main__.D at 0x10e0e53f8>, <class __main__.C at 0x10e0e5460>)
1

MRO 的 DFS 顺序如下图：

3

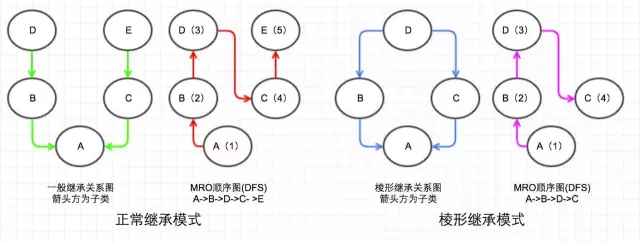
两种继承模式在 DFS 下的优缺点。
第一种，我称为正常继承模式，两个互不相关的类的多继承，这种情况 DFS 顺序正常，不会引起任何问题；

第二种，棱形继承模式，存在公共父类（D）的多继承（有种 D 字一族的感觉），这种情况下 DFS 必定经过公共父类（D），这时候想想，如果这个公共父类（D）有一些初始化属性或者方法，但是子类（C）又重写了这些属性或者方法，那么按照 DFS 顺序必定是会先找到 D 的属性或方法，那么 C 的属性或者方法将永远访问不到，导致 C 只能继承无法重写（override）。这也就是为什么新式类不使用 DFS 的原因，因为他们都有一个公共的祖先 object。

  • Python2.2 版本：新式类（new-style class）诞生

为了使类和内置类型更加统一，引入了新式类。新式类的每个类都继承于一个基类，可以是自定义类或者其它类，默认继承于 object。子类可以调用父类的构造函数。

这时有两种 MRO 的方法

  1. 如果是经典类 MRO 为 DFS（深度优先搜索（子节点顺序：从左到右））。
  2. 如果是新式类 MRO 为 BFS（广度优先搜索（子节点顺序：从左到右））。
Class A(object):   # 继承于object
    def __init__(self): print "这是新式类" A.__mro__ 可以查看新式类的顺序
1
2

MRO 的 BFS 顺序如下图：

2

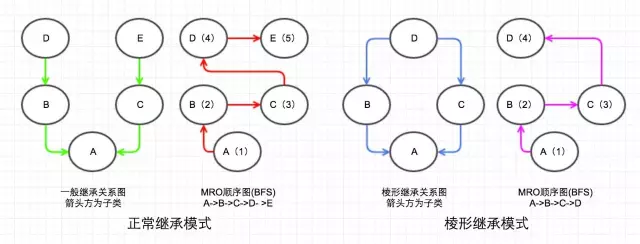
两种继承模式在 BFS 下的优缺点。
第一种，正常继承模式，看起来正常，不过实际上感觉很别扭，比如 B 明明继承了 D 的某个属性（假设为 foo），C 中也实现了这个属性 foo，那么 BFS 明明先访问 B 然后再去访问 C，但是为什么 foo 这个属性会是 C？这种应该先从 B 和 B 的父类开始找的顺序，我们称之为单调性。

第二种，棱形继承模式，这种模式下面，BFS 的查找顺序虽然解决了 DFS 顺序下面的棱形问题，但是它也是违背了查找的单调性。

因为违背了单调性，所以 BFS 方法只在 Python2.2 中出现了，在其后版本中用 C3 算法取代了 BFS。

  • Python2.3 到 Python2.7：经典类、新式类和平发展

因为之前的 BFS 存在较大的问题，所以从 Python2.3 开始新式类的 MRO 取而代之的是 C3 算法，我们可以知道 C3 算法肯定解决了单调性问题，和只能继承无法重写的问题。C3 算法具体实现稍后讲解。

MRO 的 C3 算法顺序如下图：看起简直是 DFS 和 BFS 的合体有木有。但是仅仅是看起来像而已。

3

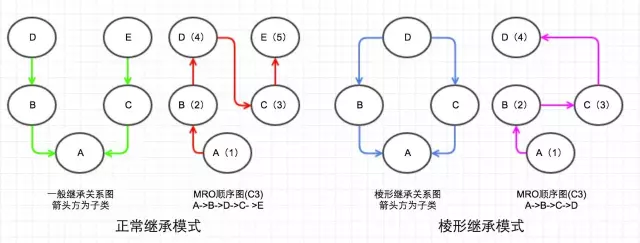
  • Python3 到至今：新式类一统江湖

Python3 开始就只存在新式类了，采用的 MRO 也依旧是 C3 算法。

# 神奇的算法 C3

take the head of the first list, i.e L[B1][0]; if this head is not in the tail of any of the other lists, then add it to the linearization of C and remove it from the lists in the merge, otherwise look at the head of the next list and take it, if it is a good head. Then repeat the operation until all the class are removed or it is impossible to find good heads. In this case, it is impossible to construct the merge, Python 2.3 will refuse to create the class C and will raise an exception.

C3 算法的本质就是 Merge，不断地把 mro()函数返回的序列进行 Merge，规则如下：

  1. 如果第一个序列的第一个元素，是后续序列的第一个元素，或者不再后续序列中再次出现，则将这个元素合并到最终的方法解析顺序序列中，并从当前操作的全部序列中删除。

  2. 如果不符合，则跳过此元素，查找下一个列表的第一个元素，重复 1 的判断规则

使用第一段代码逐步进行方法解析：

1.先打印 NewStyleClassB 和 NewStyleClassC 的 mro()，得到他们的继承顺序序列

[<class '__main__.NewStyleClassB'>, <class '__main__.NewStyleClassA'>, <class 'object'>]
[<class '__main__.NewStyleClassC'>, <class 'object'>]
1
2

2.根据 C3 算法逐步对继承顺序进行解析：


mro(SubNewStyleClass)
    = [SubNewStyleClass] + merge(mro(NewStyleClassB), mro(NewStyleClassC), [NewStyleClassB, NewStyleClassC])
    # 根据第一步的打印结果，可以得出
    = [SubNewStyleClass] + merge([NewStyleClassB, NewStyleClassA, object],  [NewStyleClassC, NewStyleClassA, object], [NewStyleClassB, NewStyleClassC])
    # 判断merge的当前序列第一个元素 NewStyleClassB, 在第三个序列中的第一个元素也存在，所以将其合并到最终序列并且删除：
    = [SubNewStyleClass, NewStyleClassB] + merge([NewStyleClassA, object],  [NewStyleClassC, NewStyleClassA, object], [NewStyleClassC])
    # 判断merge的当前序列第一个元素 NewStyleClassA，在第二个序列中存在，并且不为第二个序列的第一个元素，则跳过
    #  继续判断第二个序列中的第一个元素 NewStyleClassC，在第三个序列中存在，并且为第一个元素，所以将其合并到最终序列并且删除：
    = [SubNewStyleClass, NewStyleClassB, NewStyleClassC] + merge([NewStyleClassA, object], [NewStyleClassA, object])
    # 目前第一个序列的第一个元素是NewStyleClassA，所以再次对NewStyleClassA进行判断。
    # NewStyleClassA在第二个序列中存在，并且为第二个序列的第一个元素，所以将其合并到最终序列并且删除：
    = [SubNewStyleClass, NewStyleClassB, NewStyleClassC, NewStyleClassA] + merge([object], [object])
    # 最终object，在第二个序列中出现，并且为第一个元素，所以将其合并到最终的序列并且删除，得到最终的继承顺序：
    = [SubNewStyleClass, NewStyleClassB, NewStyleClassC, NewStyleClassA, object)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

解析的结果和调用 SubNewStyleClass.mro()方法打印出的结果是相同的：

[<class '__main__.SubNewStyleClass'>, <class '__main__.NewStyleClassB'>, <class '__main__.NewStyleClassC'>, <class '__main__.NewStyleClassA'>, <class 'object'>]
1

使用第二段代码逐步进行方法解析：

  1. 先打印 NewStyleClassB 和 NewStyleClassC 的 mro()，得到他们的继承顺序序列
[<class '__main__.NewStyleClassB'>, <class '__main__.NewStyleClassA'>, <class 'object'>]
[<class '__main__.NewStyleClassC'>, <class 'object'>]
1
2
  1. 根据 C3 算法逐步对继承顺序进行解析：

mro(SubNewStyleClass)
　　= [SubNewStyleClass] + merge(mro(NewStyleClassB), mro(NewStyleClassC), [NewStyleClassB, NewStyleClassC])
　　# 根据第一步的打印结果，可以得出
　　= [SubNewStyleClass] + merge([NewStyleClassB, NewStyleClassA, object],  [NewStyleClassC, object], [NewStyleClassB, NewStyleClassC])
　　# 判断merge的当前序列第一个元素 NewStyleClassB, 在第三个序列中的第一个元素也存在，所以将其合并到最终序列并且删除：
　　= [SubNewStyleClass, NewStyleClassB] + merge([NewStyleClassA, object],  [NewStyleClassC, object], [NewStyleClassC])
　　# 判断merge的当前序列第一个元素 NewStyleClassA，在后续的序列中都不存在，所以将其合并到最终的序列并且删除：
　　= [SubNewStyleClass, NewStyleClassB, NewStyleClassA] + merge([object], [NewStyleClassC, object], [NewStyleClassC])
　　# 判断merge的当前序列第一个元素 object，在第二个序列中出现，并且不是第一个元素，则跳过
　　# 跳过object后，继续判断下个序列的第一个元素，也就是第二个序列的第一个元素NewStyleClassC，在第三个序列中出现并且为第一个元素，所以将其合并到最终的序列并且删除：
　　= [SubNewStyleClass, NewStyleClassB, NewStyleClassA, NewStyleClassC] + merge([object], [object])
　　# 再次判断object，在第二个序列中出现，并且为第一个元素，所以将其合并到最终的序列并且删除，得到最终的继承顺序：
　　= [SubNewStyleClass, NewStyleClassB, NewStyleClassA, NewStyleClassC, object)
1
2
3
4
5
6
7
8
9
10
11
12
13
14

和调用 SubNewStyleClass.mro()方法打印出的结果是相同的

[<class '__main__.SubNewStyleClass'>, <class '__main__.NewStyleClassB'>, <class '__main__.NewStyleClassA'>, <class '__main__.NewStyleClassC'>, <class 'object'>]
1

C3 算法解决了单调性问题和只能继承无法重写问题，在很多技术文章包括官网中的 C3 算法，都只有那个 merge list 的公式法，想看的话网上很多，自己可以查。但是从公式很难理解到解决这个问题的本质。我经过一番思考后，我讲讲我所理解的 C3 算法的本质。如果错了，希望有人指出来。

假设继承关系如下(官网的例子)：

class D(object):
    pass

class E(object):
    pass

class F(object):
    pass

class C(D, F):
    pass

class B(E, D):
    pass

class A(B, C):
    pass

if __name__ == '__main__':
    print(A.__mro__)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

首先假设继承关系是一张图（事实上也是），我们按类继承是的顺序（class A(B, C)括号里面的顺序 B，C），子类指向父类，构一张图。

1

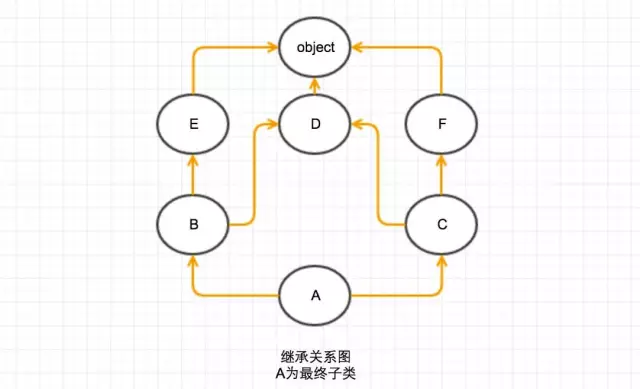
我们要解决两个问题：单调性问题和不能重写的问题。

很容易发现要解决单调性，只要保证从根(A)到叶(object)，从左到右的访问顺序即可。

那么对于只能继承，不能重写的问题呢？先分析这个问题的本质原因，主要是因为先访问了子类的父类导致的。那么怎么解决只能先访问子类再访问父类的问题呢？如果熟悉图论的人应该能马上想到拓扑排序，这里引用一下百科的的定义:

对一个有向无环图(Directed Acyclic Graph 简称 DAG)G 进行拓扑排序，是将 G 中所有顶点排成一个线性序列，使得图中任意一对顶点 u 和 v，若边(u,v)∈E(G)，则 u 在线性序列中出现在 v 之前。通常，这样的线性序列称为满足拓扑次序(Topological Order)的序列，简称拓扑序列。简单的说，由某个集合上的一个偏序得到该集合上的一个全序，这个操作称之为拓扑排序。

因为拓扑排序肯定是根到叶（也不能说是叶了，因为已经不是树了），所以只要满足从左到右，得到的拓扑排序就是结果，关于拓扑排序算法，大学的数据结构有教，这里不做讲解，不懂的可以自行谷歌或者翻一下书，建议了解完算法再往下看。

那么模拟一下例子的拓扑排序：首先找入度为 0 的点，只有一个 A，把 A 拿出来，把 A 相关的边剪掉，再找下一个入度为 0 的点，有两个点（B,C）,取最左原则，拿 B，这是排序是 A→B，然后剪 B 相关的边，这时候入度为 0 的点有 E 和 C，取最左。这时候排序为 A→B→E，接着剪 E 相关的边，这时只有一个点入度为 0，那就是 C，取 C，顺序为 A→B→E→C。剪 C 的边得到两个入度为 0 的点（DF），取最左 D，顺序为 A→B→E→C→D，然后剪 D 相关的边，那么下一个入度为 0 的就是 F，然后是 object。那么最后的排序就为 A→B→E→C→D→F→object。

对比一下 A.__mro__的结果

(<class '__main__.A'>, <class '__main__.B'>, <class '__main__.E'>, <class '__main__.C'>, <class '__main__.D'>, <class '__main__.F'>, <type 'object'>)
1

# Python 多继承详解

class A(object):    # A must be new-style class
   def __init__(self):
    print "enter A"
    print "leave A"
 
class B(C):     # A --> C
   def __init__(self):
    print "enter B"
    super(B, self).__init__()
    print "leave B"
1
2
3
4
5
6
7
8
9
10

在我们的印象中，对于 super(B, self).init()是这样理解的：super(B, self)首先找到 B 的父类（就是类 A），然后把类 B 的对象 self 转换为类 A 的对象，然后“被转换”的类 A 对象调用自己的__init__函数。

有一天某同事设计了一个相对复杂的类体系结构（我们先不要管这个类体系设计得是否合理，仅把这个例子作为一个题目来研究就好），代码如下

# 代码段4：

class A(object):
    def __init__(self):
        print "enter A"
        print "leave A"
 
class B(object):
    def __init__(self):
        print "enter B"
        print "leave B"
 
class C(A):
    def __init__(self):
        print "enter C"
        super(C, self).__init__()
        print "leave C"
 
class D(A):
    def __init__(self):
        print "enter D"
        super(D, self).__init__()
        print "leave D"

class E(B, C):
    def __init__(self):
        print "enter E"
        B.__init__(self)
        C.__init__(self)
        print "leave E"
 
class F(E, D):
    def __init__(self):
        print "enter F"
        E.__init__(self)
        D.__init__(self)
        print "leave F"
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

f = F() ，结果如下：

enter F enter E enter B leave B enter C enter D enter A leave A leave D leave C leave E enter D enter A leave A leave D leave F
1

明显地，类 A 和类 D 的初始化函数被重复调用了 2 次，这并不是我们所期望的结果！我们所期望的结果是最多只有类 A 的初始化函数被调用 2 次——其实这是多继承的类体系必须面对的问题。我们把代码段 4 的类体系画出来，如下图：

    object  
   |       \\  
   |        A  
   |      / |  
   B  C  D  
    \\   /   |  
      E    |  
        \\   |  
          F
1
2
3
4
5
6
7
8
9

按我们对super的理解，从图中可以看出，在调用类 C 的初始化函数时，应该是调用类 A 的初始化函数，但事实上却调用了类 D 的初始化函数。好一个诡异的问题！

也就是说，mro 中记录了一个类的所有基类的类类型序列。查看 mro 的记录，发觉包含 7 个元素，7 个类名分别为：

 F E B C D A object
1

从而说明了为什么在C.__init__中使用super(C, self).__init__()会调用类 D 的初始化函数了。 ???

我们把代码段 4 改写为：

# 代码段5：
class A(object):
    def __init__(self):
        print "enter A"
        super(A, self).__init__()  # new
        print "leave A"
 
class B(object):
    def __init__(self):
        print "enter B"
        super(B, self).__init__()  # new
        print "leave B"
 
class C(A):
    def __init__(self):
        print "enter C"
        super(C, self).__init__()
        print "leave C"
 
class D(A):
    def __init__(self):
        print "enter D"
        super(D, self).__init__()
        print "leave D"
        
class E(B, C):
    def __init__(self):
        print "enter E"
        super(E, self).__init__()  # change
        print "leave E"
 
class F(E, D):
    def __init__(self):
        print "enter F"
        super(F, self).__init__()  # change
        print "leave F"
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

f = F()，执行结果：

enter F enter E enter B enter C enter D enter A leave A leave D leave C leave B leave E leave F
1

可见，F 的初始化不仅完成了所有的父类的调用，而且保证了每一个父类的初始化函数只调用一次。

# 小结

1. super 并不是一个函数，是一个类名，形如 super(B, self)事实上调用了 super 类的初始化函数，产生了一个 super 对象；
　　2. super 类的初始化函数并没有做什么特殊的操作，只是简单记录了类类型和具体实例；
　　3. super(B, self).func 的调用并不是用于调用当前类的父类的 func 函数；
　　4. Python 的多继承类是通过 mro 的方式来保证各个父类的函数被逐一调用，而且保证每个父类函数只调用一次（如果每个类都使用 super）；
　　5. 混用 super 类和非绑定的函数是一个危险行为，这可能导致应该调用的父类函数没有调用或者一个父类函数被调用多次。

# 相关链接

编辑 (opens new window)
#MRO
上次更新: 2024-07-15, 03:27:09
Python 受推崇的 super
(译)Python 魔法方法指南

← (译)Python 魔法方法指南→

最近更新
01
工作
07-15
02
如何选房子
06-25
03
新版「一人企业方法论」
05-29
更多文章>
Theme by Vdoing | Copyright © 2019-2024 IMOYAO | 别院牧志